动态规划功能强大,它能够解决子问题并使用这些答案来解决大问题。但
仅当每个子问题都是离散的,即不依赖于其他子问题时,动态规划才管用。
比如,想去以下地方旅游4天,假设将埃菲尔铁塔加入“背包”后,卢浮宫将
更“便宜”:只要1天时间,而不是1.5天。用动态规划对这种情况建模呢?
这是没办法建模的,因为存在依赖关系。
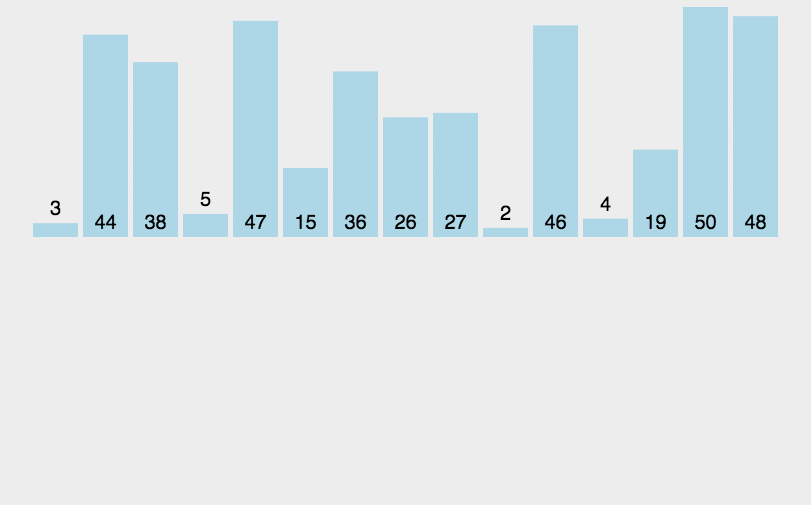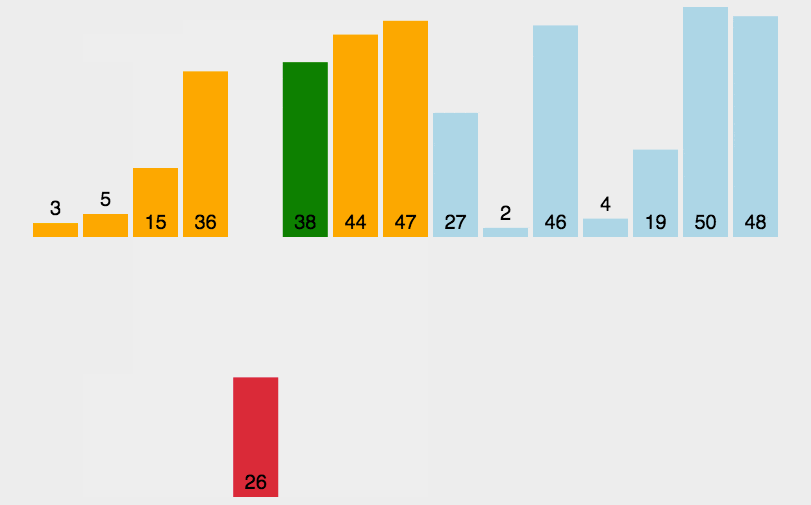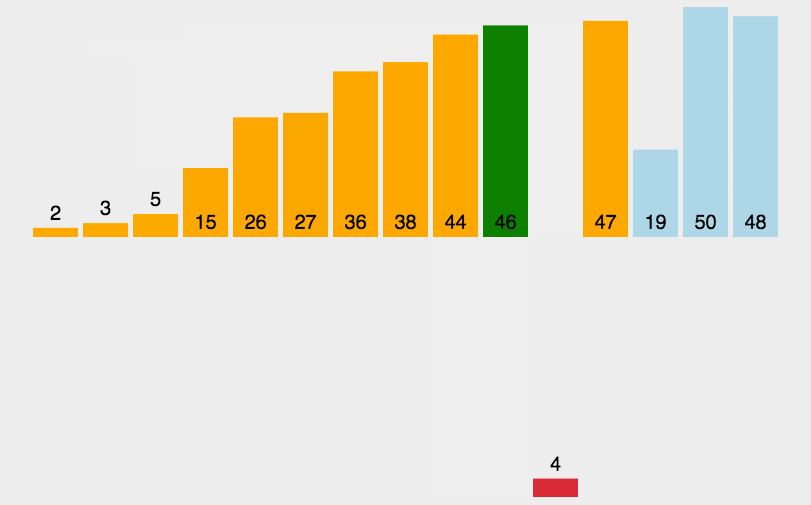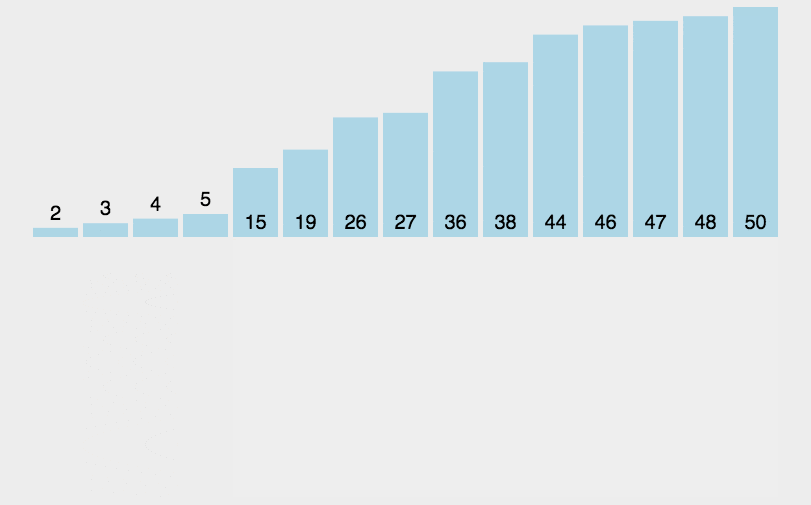
一、冒泡排序

1
2
3
4
5
6
|
def bubble_sort(arr):
for i in range(0, len(arr)): # 对每个元素
for j in range(1, len(arr)-i): # 最大的往上冒,冒完需要减1避免再次计算该值
if arr[j] > arr[j+1]: # 此处,">"为大的数往上冒,"<"为小的数往上冒
arr[j], arr[j+1] = arr[j+1], arr[j] # 交换位置
return a
|
二、选择排序

1
2
3
4
5
6
7
8
9
|
def selection_sort(arr):
for i in range(len(arr)-1): # 减1是为了第2个for的起始i+1
min_index = i
for j in range(i+1, len(arr)): # 遍历后面的值,并记录最小值的索引
if arr[min_index] > arr[j]: # 要是取最大值的索引,则改">"为"<"
min_index = j
if i != min_index: # 如果已经改变了最小索引,则交换
arr[min_index], arr[i] = arr[i], arr[min_index]
return arr
|
三、插入排序

1
2
3
4
5
6
7
8
9
|
def insertion_sort(arr):
for i in range(len(arr)):
pre_index = i-1 # 获得前一个索引
current = arr[i] # 得到当前的值
while pre_index >= 0 and arr[pre_index] > current: # 每个arr[i]值与前面的比
arr[pre_index+1] = arr[pre_index]
pre_index -= 1
arr[pre_index+1] = current # +1 可以理解为防止pre_index为 -1
return arr
|
四、希尔排序
1
2
3
4
5
6
7
8
9
|
class Solution(object):
def maxSubArray(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
for i in range(1, len(nums)):
nums[i] += max(nums[i-1], 0)
return max(nums)
|
五、归并排序
1
2
3
4
5
6
7
8
9
|
class Solution(object):
def maxSubArray(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
for i in range(1, len(nums)):
nums[i] += max(nums[i-1], 0)
return max(nums)
|
六、快速排序
1
2
3
4
5
6
7
8
9
|
class Solution(object):
def maxSubArray(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
for i in range(1, len(nums)):
nums[i] += max(nums[i-1], 0)
return max(nums)
|
七、堆排序
1
2
3
4
5
6
7
8
9
|
class Solution(object):
def maxSubArray(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
for i in range(1, len(nums)):
nums[i] += max(nums[i-1], 0)
return max(nums)
|
八、计数排序
1
2
3
4
5
6
7
8
9
|
class Solution(object):
def maxSubArray(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
for i in range(1, len(nums)):
nums[i] += max(nums[i-1], 0)
return max(nums)
|
九、桶排序
1
2
3
4
5
6
7
8
9
|
class Solution(object):
def maxSubArray(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
for i in range(1, len(nums)):
nums[i] += max(nums[i-1], 0)
return max(nums)
|
十、基数排序
1
2
3
4
5
6
7
8
9
|
class Solution(object):
def maxSubArray(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
for i in range(1, len(nums)):
nums[i] += max(nums[i-1], 0)
return max(nums)
|